This is the first post in a series about sport climbing at the 2020 Summer Olympics. In this post, I’m going to conduct a simple simulation study to examine scoring and rankings for Olympics climbers.
Introduction
Sport climbing at the 2020 Summer Olympics in Tokyo, Japan begins August 3. It is one of the five new sports introduced at Tokyo 2020, alongside baseball/softball, karate, skateboarding, and surfing. Sport climbing at Tokyo 2020 consists of two events, one for male and one for female, with only one set of medal being awarded per gender. Each event includes two phases: qualification and finals. For each round, climbers compete in three disciplines: speed climbing, bouldering, and lead climbing. Both men’s and women’s competition begin with 20 climbers, with 8 being selected to move on to the final stage, based on rankings. A climber’s performance is determined by a combined score, which is computed as a the product of the ranks across three disciplines. At the end of each round, athletes are ranked based on their combined scores, meaning that the 8 climbers with the lowest product of ranks advance to the finals and the top 3 finalists with the lowest rank product win gold, silver, and bronze, respectively.
The focus of this post is going to be on a simulation study examining the performances of climbers in both qualification and finals. 10000 simulations are executed for each round, as the event ranks (1-20 for qualification, 1-8 for finals) are randomly assigned to the athletes, assuming a uniform distribution for the ranks. The final scores and final rankings are also going to be calculated, and I’m going to utilize this data to answer questions regarding scoring and probability of finishing at certain ranking positions.
Data Prep
library(tidyverse)
library(kableExtra)
theme_set(theme_light())
Let’s first write a function to simulate the climbing competitions for any given number of climbers. This function takes in the number of simulations and players and returns a simulated data frame with the following attributes: player ID, the rank for each discipline, final combined score, final rank, and simulation number. In this particular case, I’m going to use this function to simulate both qualification (20 climbers) and final (8 climbers) rounds of sport climbing.
climbing_sim <- function(nsim = 10000, nplay) {
sims <- list()
for (i in 1:nsim) {
sims[[i]] <-
bind_cols(
player = 1:nplay,
e1 = sample(1:nplay, replace = FALSE),
e2 = sample(1:nplay, replace = FALSE),
e3 = sample(1:nplay, replace = FALSE)
) %>%
mutate(sim = i)
}
results <- bind_rows(sims) %>%
mutate(score = e1 * e2 * e3) %>%
group_by(sim) %>%
mutate(rank = rank(score, ties.method = "random")) %>%
ungroup()
return(results)
}
set.seed(1)
qual <- climbing_sim(nsim = 10000, nplay = 20)
final <- climbing_sim(nsim = 10000, nplay = 8)
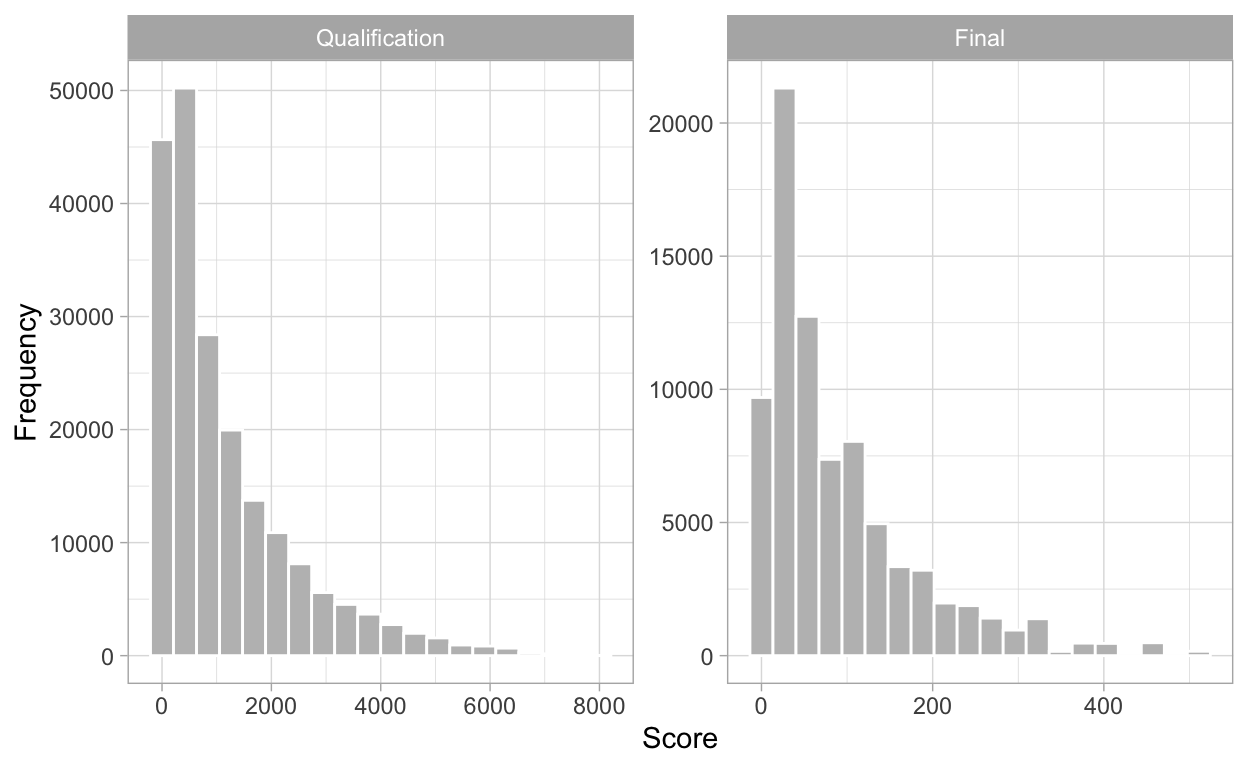
To get the analysis stage started, here are visual and numerical summaries of the total scores obtained from our simulations for qualification and final rounds.
Show code
qual_final <- qual %>%
mutate(round = "Qualification") %>%
bind_rows(mutate(final, round = "Final")) %>%
mutate(round = fct_rev(round))
qual_final %>%
ggplot(aes(score)) +
geom_histogram(bins = 20, fill = "gray", color = "white") +
facet_wrap(~ round, scales = "free") +
labs(x = "Score",
y = "Frequency")
Show code
| round | min | Q1 | median | Q3 | max | mean | sd | n |
|---|---|---|---|---|---|---|---|---|
| Qualification | 1 | 240 | 684 | 1638 | 8000 | 1158.84378 | 1273.47884 | 200000 |
| Final | 1 | 24 | 60 | 126 | 512 | 91.19935 | 91.11065 | 80000 |
Qualification
Let’s begin with a simple question: “If a climber wins any event, what is the probability that they advance to the finals?”
In the table below, the column rank represents the every possible qualification finishing position, given that a climber wins at least one event. For each rank, given that a contestant wins any event, n is the number of times that climbers finish at the given rank, prob is the probability of finishing at exactly the given rank, and cum_prob is the probability of finishing at or below the given rank.
Show code
| rank | n | prob | cum_prob |
|---|---|---|---|
| 1 | 7890 | 0.2761735 | 0.2761735 |
| 2 | 5943 | 0.2080227 | 0.4841962 |
| 3 | 4644 | 0.1625538 | 0.6467500 |
| 4 | 3651 | 0.1277959 | 0.7745458 |
| 5 | 2766 | 0.0968182 | 0.8713641 |
| 6 | 1960 | 0.0686058 | 0.9399699 |
| 7 | 1118 | 0.0391333 | 0.9791032 |
| 8 | 448 | 0.0156813 | 0.9947846 |
| 9 | 127 | 0.0044454 | 0.9992299 |
| 10 | 19 | 0.0006651 | 0.9998950 |
| 11 | 3 | 0.0001050 | 1.0000000 |
Show code
win_any_qual %>%
ggplot(aes(rank, weight = prob)) +
geom_bar(fill = c(rep("gray", 8), rep("black", 3))) +
geom_vline(xintercept = 8.5) +
scale_x_continuous(breaks = 1:11) +
scale_y_continuous(limits = c(0, 0.3)) +
labs(x = "Rank",
y = "Probability",
title = "Probability of finishing at every rank given winning any event")
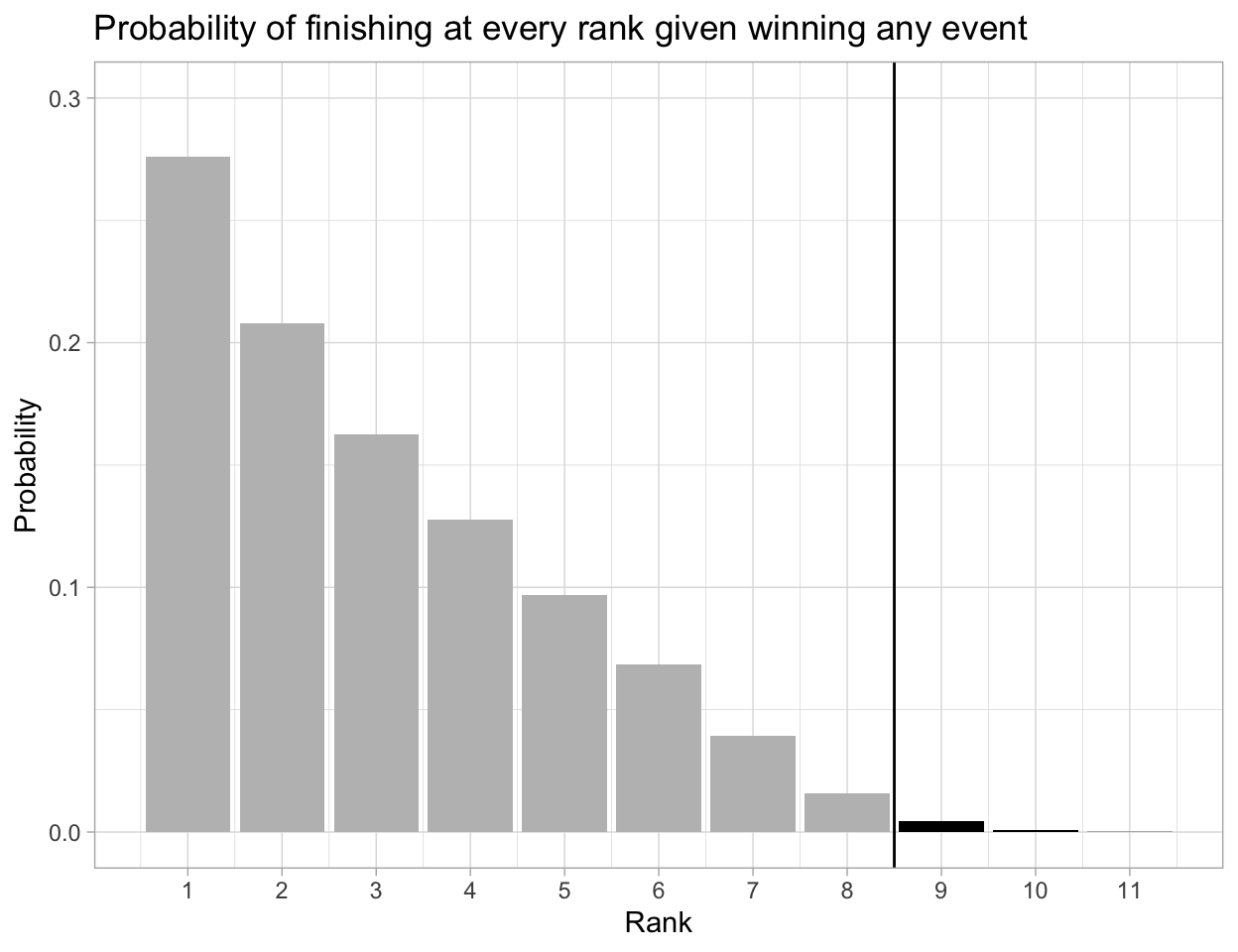
It is clear that a climber will certainly book their ticket to the final round if they win any event, as the probability of finishing at 8th or lower is 0.9948, very close to a perfect 100%.
What if we just focus on winning the first event (speed, in real life)? How often do climbers advance?
Show code
| rank | n | prob | cum_prob |
|---|---|---|---|
| 1 | 2999 | 0.2999 | 0.2999 |
| 2 | 1963 | 0.1963 | 0.4962 |
| 3 | 1559 | 0.1559 | 0.6521 |
| 4 | 1269 | 0.1269 | 0.7790 |
| 5 | 957 | 0.0957 | 0.8747 |
| 6 | 686 | 0.0686 | 0.9433 |
| 7 | 363 | 0.0363 | 0.9796 |
| 8 | 155 | 0.0155 | 0.9951 |
| 9 | 42 | 0.0042 | 0.9993 |
| 10 | 6 | 0.0006 | 0.9999 |
| 11 | 1 | 0.0001 | 1.0000 |
Show code
win_first_qual %>%
ggplot(aes(rank, weight = prob)) +
geom_bar(fill = c(rep("gray", 8), rep("black", 3))) +
geom_vline(xintercept = 8.5) +
scale_x_continuous(breaks = 1:11) +
scale_y_continuous(limits = c(0, 0.3)) +
labs(x = "Rank",
y = "Probability",
title = "Probability of finishing at every rank given winning the first event")
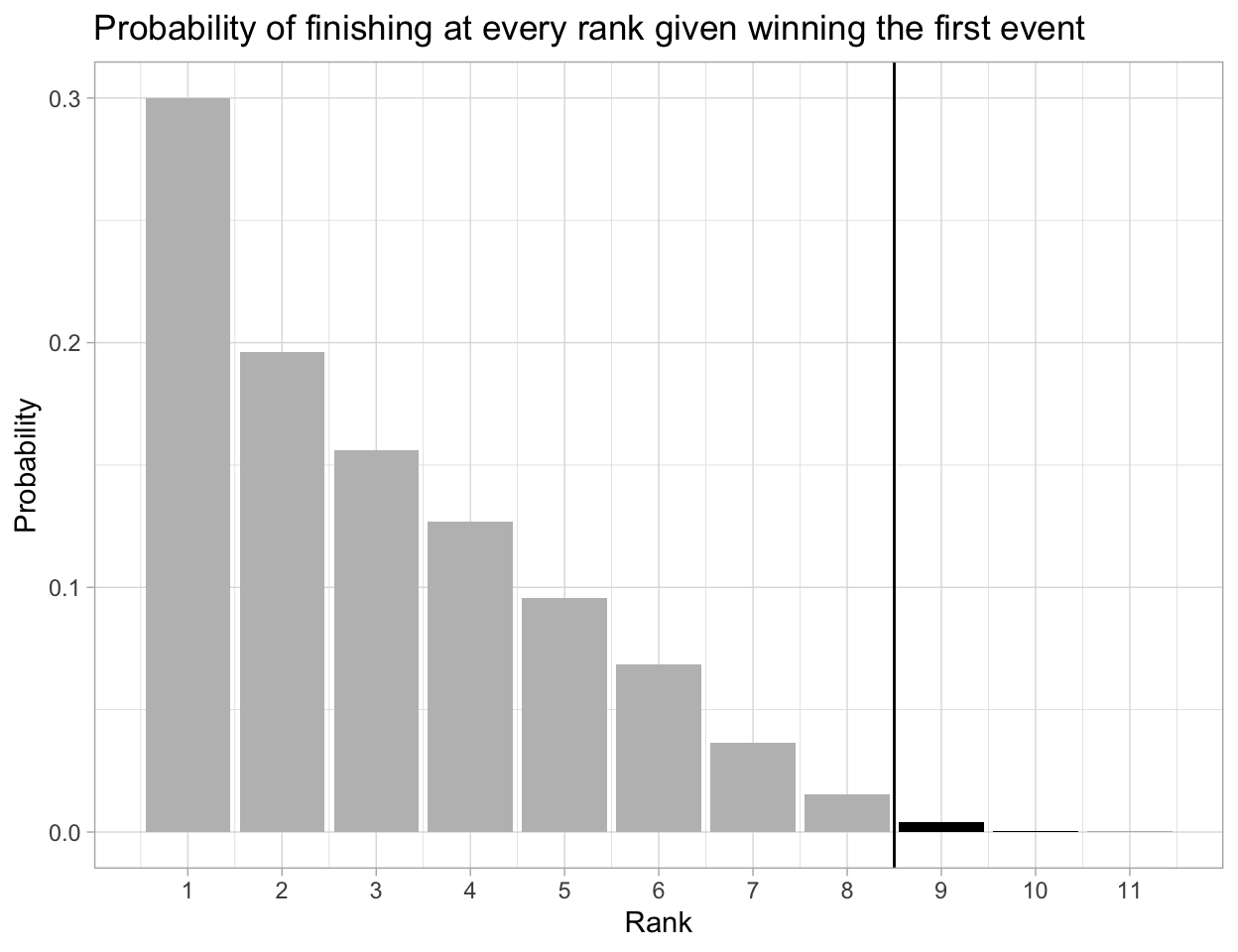
The results look very similar to the previous analysis. The probability of making to the finals given being event 1 winner for a athlete is also as close to perfect as it could get (0.9951). After winning the first event, a climber is also more likely to finish first more than any other places in the overall qualification standings (almost 30% of the times). Therefore, what climbers should be aware of is getting off to a great start in this combined competition format is crucial.
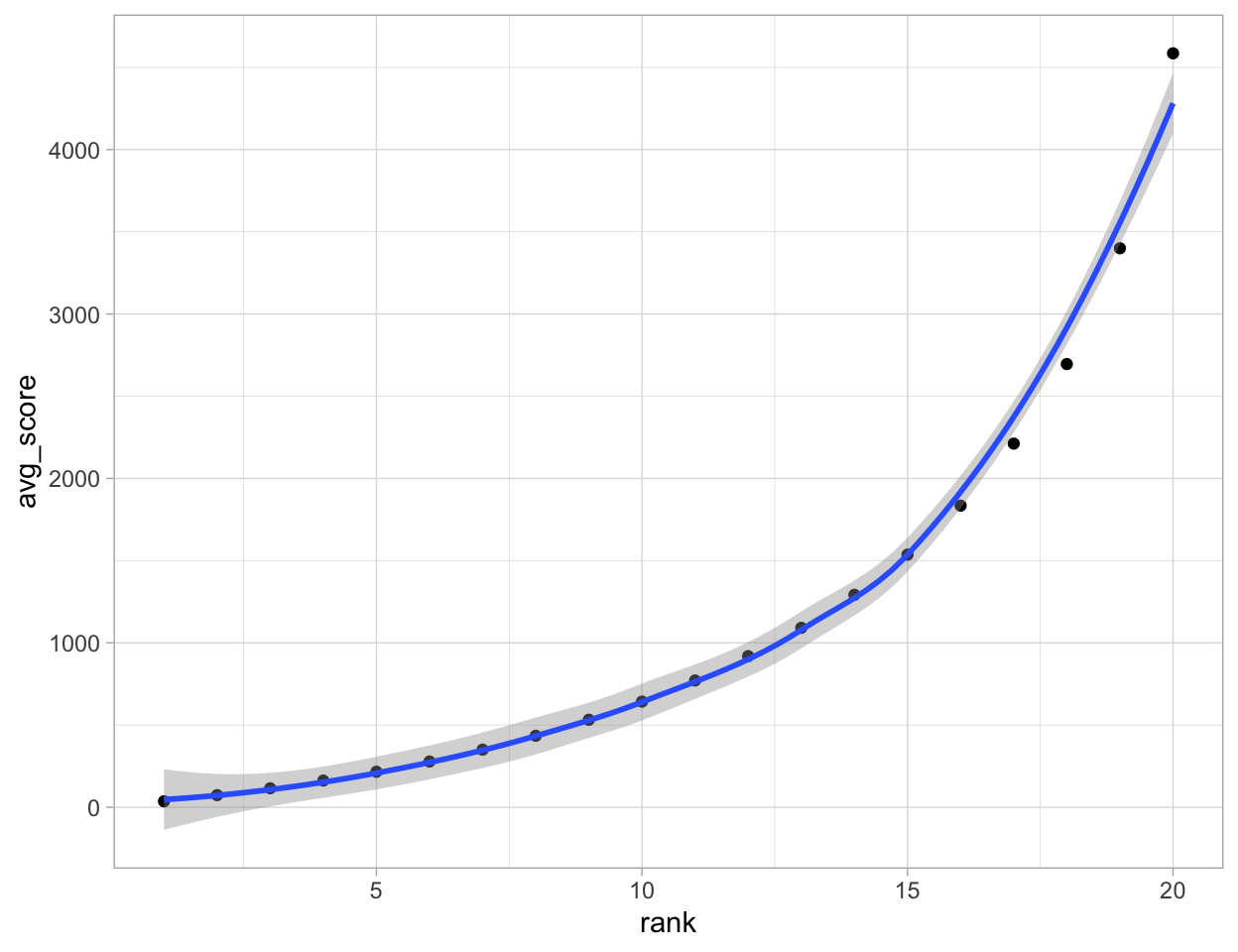
What is the average score of finalists? What is the distribution of the score for each qualification rank?
Show code
| rank | avg_score |
|---|---|
| 1 | 36.0187 |
| 2 | 73.6111 |
| 3 | 115.3954 |
| 4 | 162.2263 |
| 5 | 216.0041 |
| 6 | 278.1649 |
| 7 | 350.3272 |
| 8 | 434.5932 |
| 9 | 532.1383 |
| 10 | 642.3298 |
Show code
qual_avg %>%
ggplot(aes(x = rank, y = avg_score)) +
geom_point() +
geom_smooth()
Show code
qual %>%
mutate(rank = factor(rank)) %>%
ggplot(aes(x = rank, y = score)) +
geom_dotplot(binaxis = "y", binwidth = 1) +
coord_flip()
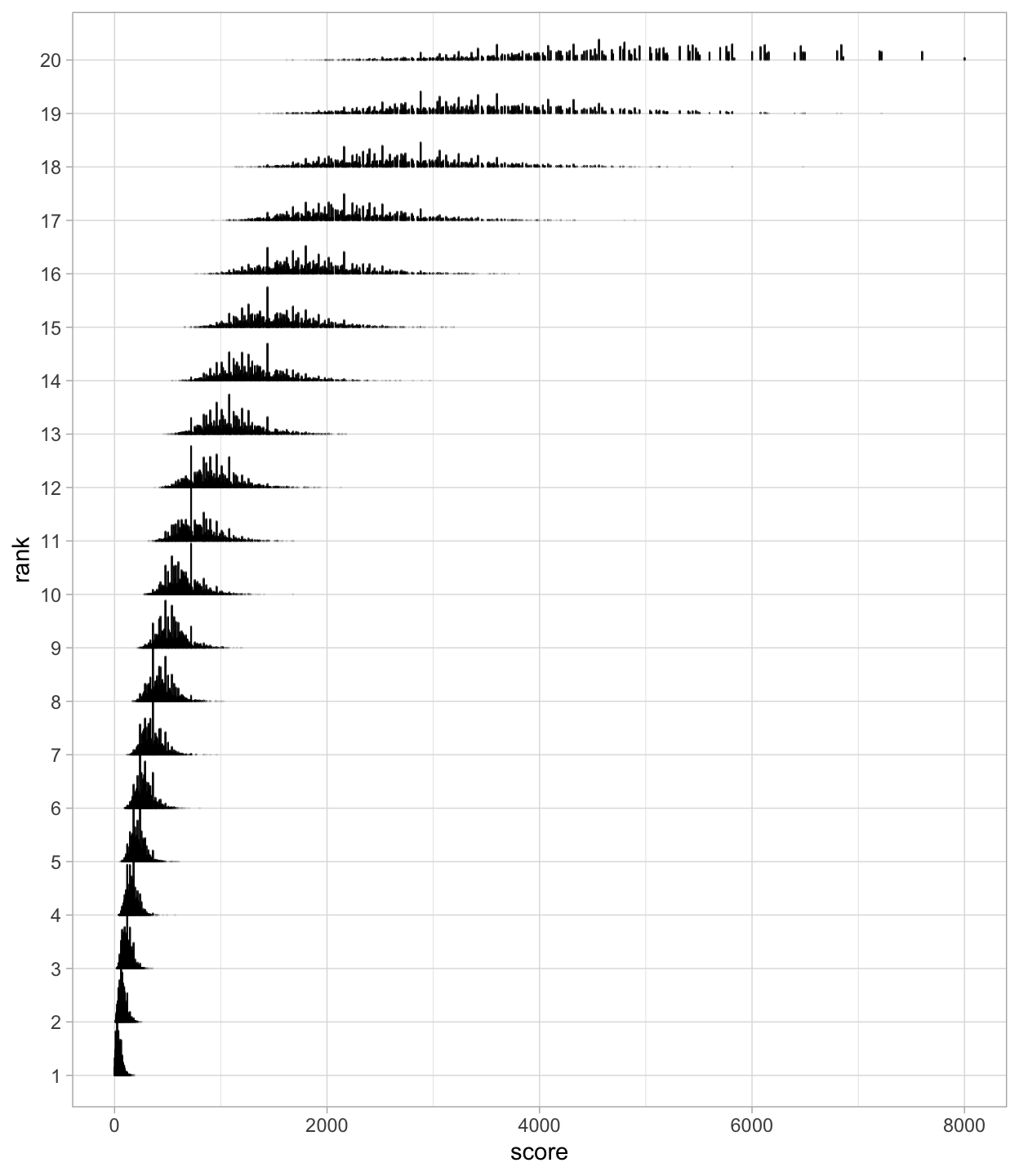
From the descriptive statistics above, the expected minimum score for finishing in the top 8 and securing a final spot is 434 (rounded down, for 8th rank). Thus, a climber should aim for a total score at or below this threshold. In addition, the plots show that as the rank increases, the distribution of the scores becomes more spread out, and the average score also grows exponentially.
Finals
Now, let’s play the same game with the final round, as I’m going to answer similar type of questions for finals as what I had earlier for qualification.
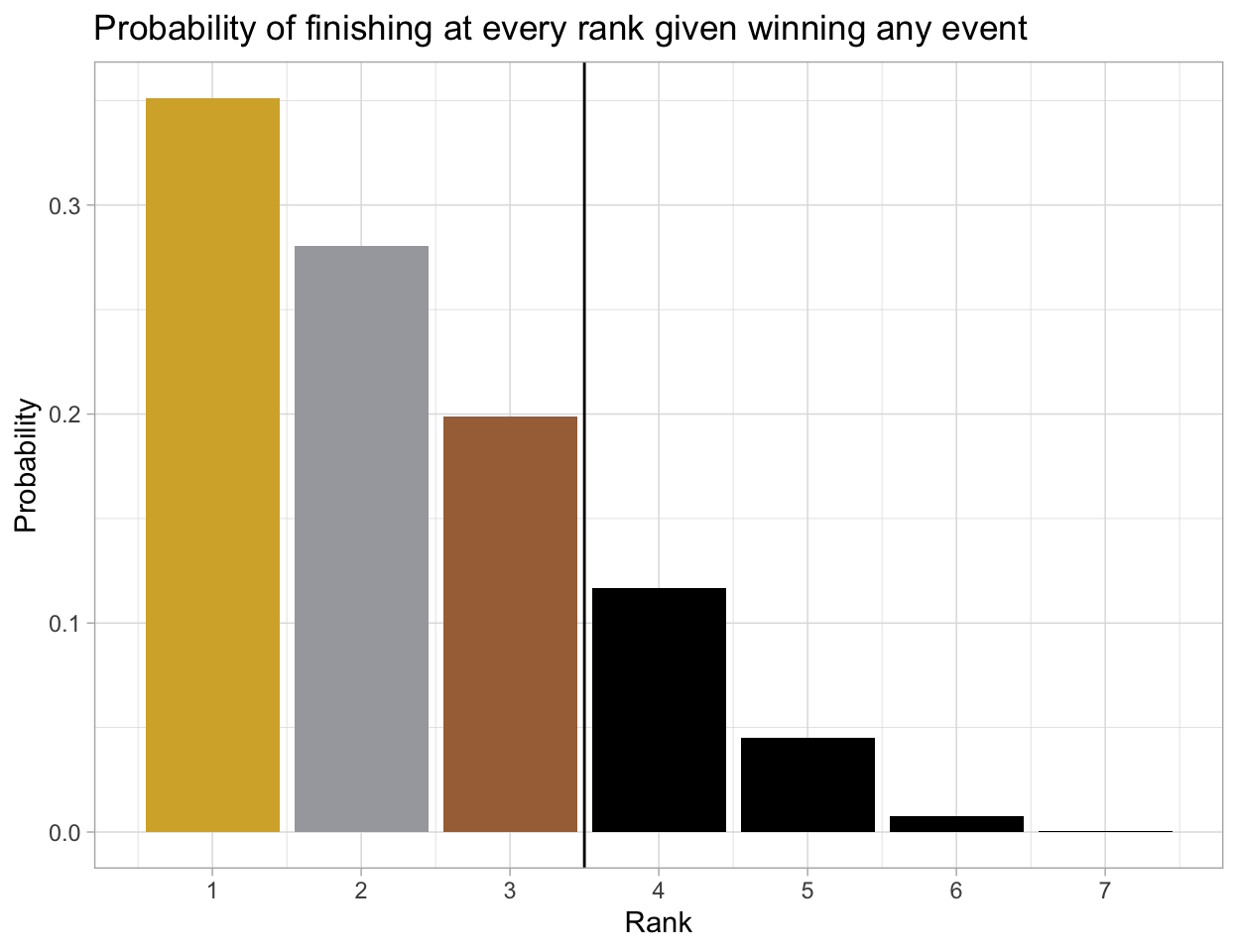
If a climber wins any event (or just the first event), what is the probability of them winning a medal?
Show code
| rank | n | prob | cum_prob |
|---|---|---|---|
| 1 | 9277 | 0.3512286 | 0.3512286 |
| 2 | 7409 | 0.2805058 | 0.6317344 |
| 3 | 5257 | 0.1990308 | 0.8307652 |
| 4 | 3078 | 0.1165335 | 0.9472987 |
| 5 | 1187 | 0.0449400 | 0.9922387 |
| 6 | 198 | 0.0074963 | 0.9997350 |
| 7 | 7 | 0.0002650 | 1.0000000 |
Show code
Show code
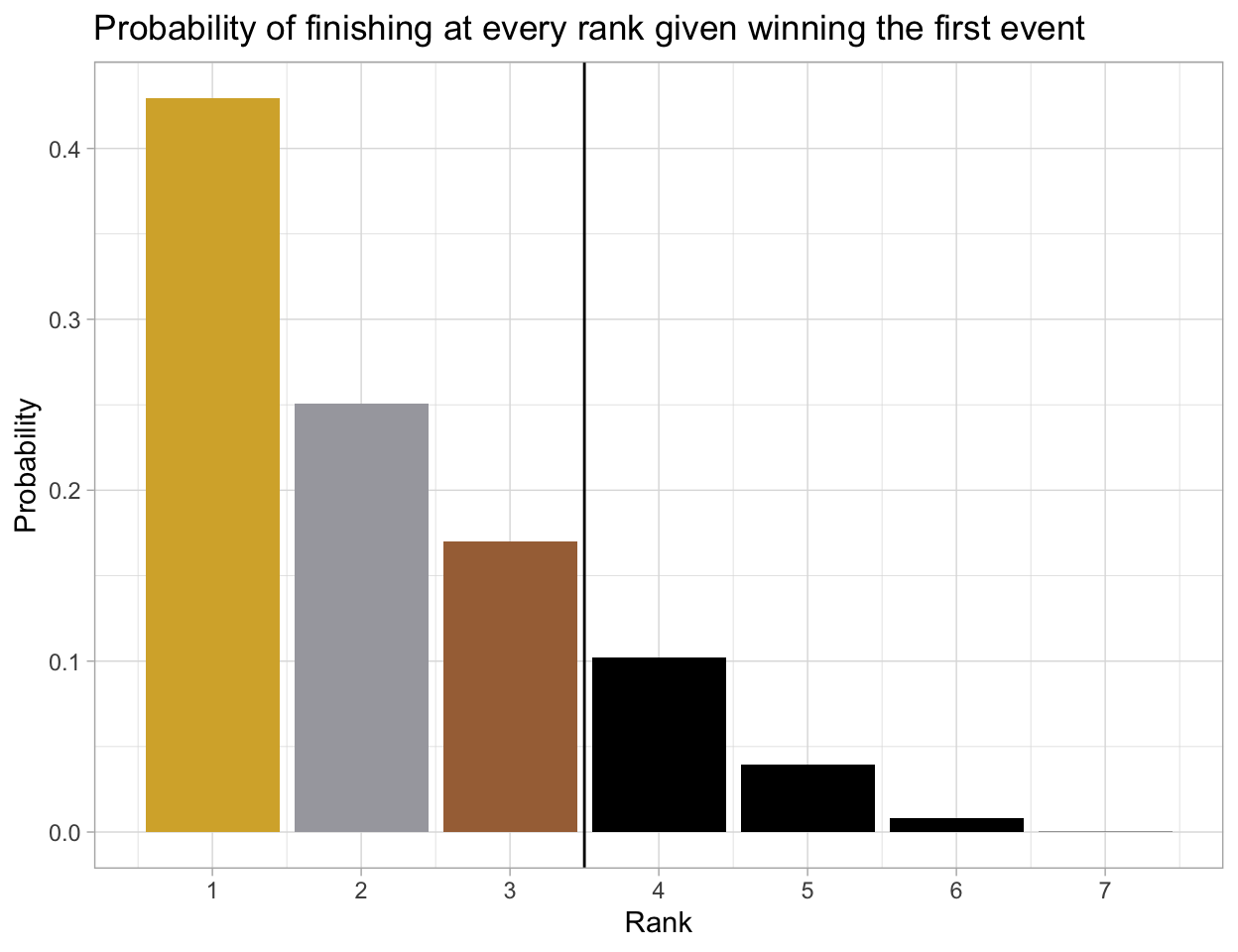
| rank | n | prob | cum_prob |
|---|---|---|---|
| 1 | 4295 | 0.4295 | 0.4295 |
| 2 | 2505 | 0.2505 | 0.6800 |
| 3 | 1702 | 0.1702 | 0.8502 |
| 4 | 1020 | 0.1020 | 0.9522 |
| 5 | 393 | 0.0393 | 0.9915 |
| 6 | 83 | 0.0083 | 0.9998 |
| 7 | 2 | 0.0002 | 1.0000 |
Show code
win_first_final %>%
ggplot(aes(rank, weight = prob)) +
geom_bar(fill = c("#D6AF36", "#A7A7AD", "#A77044", rep("black", 4))) +
geom_vline(xintercept = 3.5) +
scale_x_continuous(breaks = 1:7) +
labs(x = "Rank",
y = "Probability",
title = "Probability of finishing at every rank given winning the first event")
What is the average score of medalists?
Show code
| rank | avg_score |
|---|---|
| 1 | 9.6687 |
| 2 | 20.1844 |
| 3 | 33.3658 |
| 4 | 50.5734 |
| 5 | 75.2499 |
| 6 | 110.7070 |
| 7 | 164.8258 |
| 8 | 265.0198 |
A finalist is very likely to finish in the top 3 and stand in the tri-level podium if they win the first event (83.08% chance) or any event (85.02%). In order to bring home a climbing medal, the average score (rounded down) for getting gold, silver, and bronze are 9, 20, and 33, respectively.
Future Work
This is the end of my first post of the series on sport climbing. My next post is going to be centered around analyzing climbing data from previous competitions that used the combined rank-product scoring format. If you have any questions, or if you would like me to explore other questions related to the simulation data, please leave a comment.